Kedudukan Dua garis – Pernahkah Anda memerhatikan rel atau lintasan kereta api? Apabila kita perhatikan lintasan kereta api tersebut, jarak antara dua rel akan selalu tetap (sama) dan tidak pernah saling berpotongan antara satu dengan lainnya. Apa yang akan terjadi jika jaraknya berubah? Apakah kedua rel itu akan berpotongan?
Daftar Isi
Kedudukan Dua garis sejajar

Berdasarkan gambaran tersebut, selanjutnya apabila dua buah rel kereta api kita anggap sebagai dua buah garis, maka dapat kita gambarkan seperti gambar di bawah ini.

Garis m dan garis n di atas, jika diperpanjang sampai tak berhingga maka kedua garis tidak akan pernah berpotongan. Keadaan seperti ini dikatakan kedua garis sejajar. Dua garis sejajar dinotasikan dengan “//”.
Dua garis atau lebih dikatakan sejajar apabila garis-garis tersebut terletak pada satu bidang datar dan tidak akan pernah bertemu atau berpotongan jika garis tersebut diperpanjang sampai tak berhingga.
Dua garis berpotongan
Agar Anda memahami pengertian garis berpotongan, perhatikan gambar di bawah ini.
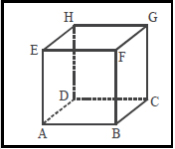
Gambar di atas tersebut menunjukkan gambar kubus ABCD.EFGH. Amatilah garis AB dan garis BC. Tampak bahwa garis AB dan BC berpotongan di titik B dimana keduanya terletak pada bidang ABCD. Dalam hal ini garis AB dan BC dikatakan saling berpotongan.
Dua garis dikatakan saling berpotongan apabila garis tersebut terletak pada satu bidang datar dan mempunyai satu titik potong.
Dua garis berimpit
Agar Anda memahami pengertian garis berimpit, perhatikan gambar di bawah ini.

Pada Gambar di atas menunjukkan garis AB dan garis CD yang saling menutupi, sehingga hanya terlihat sebagai satu garis lurus saja. Dalam hal ini dikatakan kedudukan masing-masing garis AB dan CD terletak pada satu garis lurus. Kedudukan garis yang demikian dinamakan pasangan garis yang berimpit.
Dua garis dikatakan saling berimpit apabila garis tersebut terletak pada satu garis lurus, sehingga hanya terlihat sebagai satu garis lurus saja.
Dua garis bersilangan
Agar Anda memahami pengertian garis bersilangan, perhatikan gambar di bawah ini.
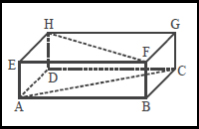
Gambar di atas menunjukkan sebuah balok ABCD.EFGH. Perhatikan garis AC dan garis HF. Tampak bahwa kedua garis tersebut tidak terletak pada satu bidang datar. Garis AC terletak pada bidang ABCD, sedangkan garis HF terletak pada bidang EFGH. Selanjutnya apabila kedua garis tersebut, masing-masing diperpanjang, maka kedua garis tidak akan pernah bertemu. Dengan kata lain, kedua garis itu tidak mempunyai titik potong. Kedudukan garis yang demikian dinamakan pasangan garis yang saling bersilangan.
Dua garis dikatakan bersilangan apabila garis-garis tersebut tidak terletak pada satu bidang datar dan tidak akan berpotongan apabila diperpanjang.
Garis Horizontal dan Garis Vertikal
Perhatikan gambar di bawah ini.
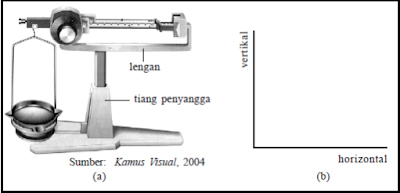
Gambar tersebut menunjukkan sebuah neraca dengan bagian-bagiannya. Perhatikan bagian tiang penyangga dan bagian lengan yang berada di atasnya. Kedudukan bagian tiang dan lengan tersebut menggambarkan garis horizontal dan vertikal. Bagian lengan menunjukkan kedudukan garis horizontal, sedangkan tiang penyangga menunjukkan kedudukan garis vertikal. Arah garis horizontal mendatar, sedangkan garis vertikal tegak lurus dengan garis horizontal.