Contoh Soal Peluang – Sebelumnya akan admin bahas dulu dari sisi bahasa Peluang atau kebolehjadian atau dengan nama lain probabilitas merupakan sebuah ilmu yang mempelari kejadian yang tentu saja telah berlalu atau terjadi.
Pada awalnya rumus peluang hanya berlaku dalam ilmu matematika saja, namun seiring perkembangan sains konsep peluang juga akan di pelajari dalam disiplin ilmu lain seperti halnya statistik sampai dengan filsafat dan fisika.
Ok pada kesempatan ini kami akan mencoba share beberapa contoh soal peluang baik dalam sebuah dadu, koin, kartu sampai dengan sebuah data statistik yang dimana akan lebih susah bisa sahabat pelajari disini.
Karena memang jenis materi matematika yang satu ini sangat biasa sekali keluar dalam ujian nasional nantinya di tingkat SMP. Supaya lebih komplit admin akan kupas tuntas tentu saja semua contoh soal peluang dan pembahasannya kelas 9 sampai 11 baik berupa kejadian majemuk dan masih banyak lagi.
Lalu apa yang dimaksud dengan Probabilitas suatu kejadian ? ya tidak lain adalah sebuah angka yang akan memberikan petunjuk dari suatu pristiwa atau kejadian yang sudah terjadi. Dimana akan disimbolkan dengan bilangan 0 dan angka 1. Dimana jika angka 1 maka sudah pastu terjadi dan jika 0 maka belum tentu bisa terjadi.
Sebagai salah satu contohnya adalah nilai probabilitas 1 misalkan saja, adanya siang malam dimana ini pasti terjadi dan jika O contohnya ketidak mungkinan seperti ayam menetaskan anak buaya dsb. Itulah sekilas tentang peluang/probabilitas dalam ilmu menghitung yang bisa kami sajikan dan dibawah ini langsung saja adik adik bisa deh melihat dan langsung memahami beberapa contoh soal peluang yang lengkap dengan jawabanya.
Contoh Soal Peluang Matematika (peluang mtk)

1.) Sebuah dadu dilempar sekali, tentukan peluang munculnya mata dadu 6!
Jawab :
Banyaknya titik sampel n(s) = 6
Titik sampel mata dadu bernilai 6 n(A) = 1
Jadi, peluang munculnya mata dadu 6 adalah 1/6
Banyaknya titik sampel n(s) = 52
Titik sampel kartu as n(A) = 4
Jadi, peluang munculnya kartu as adalah 1/13
Banyaknya titik sampel n(s) = 4 + 3 + 5 = 12
Titik sampel kelereng biru n(A) = 3
4.) Seorang pedagang telur memiliki 200 butir telur, karena kurang berhati-hati 10 butir telur pecah. Semua telur diletakan dalam peti. Jika sebutir telur diambil secara acak. Tentukan peluang terambilnya telur yang tidak pecah!
Jawab :
Banyaknya titik sampel n(s) = 200
Titik sampel telur yang tidak pecah n(A) = 200 – 10 = 190
Jadi, peluang terambilnya telur yang tidak pecah adalah 19/20
Ruang sampelnya yaitu = { (A,G), (A,A), (G,A), (G,G)}
n ( s) = 4
banyaknya titik sampel keduanya angka yaitu n (A) = 1
Peluang kejadian
Besarnya kemungkinan terjadinya sebuah kejadian disebut peluang kejadian. Penentuan nilai peluang kejadian didasarkan pada banyak anggota dan banyak anggota ruang sampelnya. Atau secara matematis penentuan nilai peluang suatu kejadian ditulis:
PK = nK / nS
Catatan:
- Untuk menentukan nK atau nS dapat menggunakan rumus permutasi atau Kombinasi:
- Permutasi dipakai jika dalam soal ada istilah jabatan, urutan, rangking, predikat, cara duduk, susunan angka.
- Kombinasi dipakai jika dalam soal ditanyakan: banyak himpunan bagian, peluang, urutan diabaikan.
Dalam percobaan pelemparan sebuah dadu setimbang, K menyatakan kejadian munculnya mata dadu bilangan genap. Peluang kejadian K adalah…
B. 1/4
C. 1/3
D. 1/2
E. 1/4
nK = 3
nS = 6
Sehingga PK = nK / nS = 3/6 = 1/2
Jawaban: D
B. 3/5
C. 1/2
D. 3/10
E. 2/5
nK = 5
nS = 10
maka PK = nK / nS = 5/10 = 1/2
Jawaban: C
B. 1/13
C. 9 / 52
D. 1/4
E. 1/3
nK = 13
nS = 52
Jadi PK = nK / nS = 13/52 = 1/4
Jawaban: D
B. 7 / 36
C . 6 / 36
D. 5 / 36
E. 4/36
B. 1/6
C. 1/4
D. 1/9
E. 5/36
nK = 4
nS = 36
Maka PK = nK / nS = 4 / 36 = 1/9
Jawaban: D
B. 1/3
C. 7/24
D. 1/4
E. 3/7
Banyak cara mengambil 3 kelereng merah dari 7 kelereng merah = nK = 7C3.
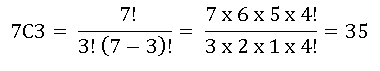
Banyak cara mengambil 3 kelereng merah dari seluruh kelereng 10 buah = nS = 10C3

Peluang terambil 3 kelereng merah nK.

B. 116/330
C. 63/330
D. 53/330
E. 27/330
Banyak cara mengambil 2 kelereng merah dari 7 kelereng = 7C2.
7C2 = 7! / (2! . 5!) = 21.Banyak cara mengambil 2 kelereng putih dari 4 kelereng = 4C2.
4C2 = 4! / (2! . 2!) = 6.Banyak cara mengambil 2 kelereng merah dan 2 kelereng putih = nK = 7C2 . 4C2 = 21 . 6 = 126.Banyak cara mengambil 4 kelereng dari seluruh kelereng (11 kelereng) = nS = 11C4.

Peluang terambil 2 kelereng merah dan kelereng putih PK.
PK = 126/330.
Jawaban: A
B. 5 / 36
C. 4 / 36
D. 3 / 36
E. 1 / 36
Merupakan peluang kejadian saling lepas:
P(3 dan 5) = P(3) x P(5) = 1/6 x 1/6 = 1 / 36
B. 1/6
C. 1/4
D. 1/3
E. 1/2
Merupakan peluang saling bebas, maka:
P(gambar dan ganjil) = P(gambar) x P(ganjil) = 1/2 x 3/6 = 3/12 = 1/4
Catatan
P(gambar) = nK / nS = 1/2
P(ganjil) = nK / nS = 3/6
B. 7 / 36
C. 8 / 36
D. 9 / 36
E. 11 / 36
Merupakan peluang kejadian saling lepas:
P(9 atau 10) = P(9) + P(10) = 4/36 + 3/36 = 7/36
Keterangan
nS (2 dadu) = 36
nK (9) = (3,6), (6,3), (4,5), (5,4) = 4
nK (10) = (4,6), (6,4), (5,5) = 3
Jadi:
P(9) = nK / nS = 4/36
P(10) = nK / nS = 3/36
Contoh Soal Peluang Dan Penyelesaiannya
Contoh soal 1.
Pada percobaan pelemparan sebuah mata uang logam sebanyak 150 kali, ternyata muncul angka sebanyak 78 kali. Tentukanlah
a. Frekuensi relatif muncul angka
b. frekunesi relatif muncul gambar
Penyelesaian :
a. Frekuensi relatif muncul angka = banyak angka yang muncul banyak percobaan
= 78 / 150
= 13/25
b. Frekuensi relatif muncul gambar = banyak gambar yang muncul banyak percobaan
= (150-78)/150
= 72/150
= 12/25
Contoh soal 2.
Apabila terdapat sebuah dadu yang dilempar undi sekali, tentukanlah peluang muncul :
a. mata dadu 4
b. mata dadu bilangan ganjil
Penyelesaian :
a. Banyaknya kejadian muncul mata dadu 4 = 1. Banyak kejadian yang mungkin = 6 yaitu muncul mata dadu 1, 2, 3, 4, 5, 6.
Sehingga, P(mata 4) = 1/6
b. Banyak kejadian muncul mata dadu bilangan ganjil = 3 yaitu mata dadu 1, 3, dan 5.
Sehingga, P(ganjil) = 3/6 = 1/2
Contoh soal 3.
Sebuah huruf dipilih secara acak dari huruf-huruf pada kata ” SURABAYA”. Tentukanlah peluang terpilihnya huruf A?
Penyelesaian :
banyak kejadian muncul huruf A = 3 karena terdapat 3 huruf pada kata tersebut.
banyak kejadian yang mungkin = 8
Sehingga, P(huruf A)= 3/8.
Contoh soal 4.
Dalam sebuah kotak terdapat 12 bola merah serta 15 bola biru. Apabila satu bola diambil secara acak. Tentukanlah peluang terambilnya bola biru.
Penyelesaian :
Banyak bola biru = 15
Jumlah seluruh bola = 12 + 15 = 27
Sehingga, P(biru) = 15/27 = 5/9
Contoh soal 5.
Dalam sebuah kotak terdapat lima buah bola yang diberi nomor 1 sampai 5. Jika sebuah bola akan diambil secara acak dari kotak tersebut.
a. Tentukanlah peluang terambilnya bola bernomor gelap.
b. Jika yang terambil bola bernomor ganjil, serta tidak dikembalikan lagi. Tentukanlah peluang terambilnya bola bernomor ganjil pada pengambilan berikutnya.
Penyelesaian :
a. Banyak bola bernomor genap ada 2 yaitu bola bernomor 2 dan 4.
Sehingga P(genap) = 2/5
b. Banyak bola bernomor ganjil ada 3, terambil 1 sehingga banyak bola bernomor ganjil sekarang 2.
Maka P(ganjil) = (3-1)/(5-1) = 2/4 = 1/2
Ok sahabat di rumah dari beberapa urain dan contoh soal peluang diatas, kalian tentu saja sudah bisa menemukan sedikit masukan dan akan menambah pengetahuan kalian dalam menjawab soal nanti. Tentu saja dalam ilmu matematika kalian haruslah bisa hafal dulu rumusnya kemudian bagaimana langkah menyelesaikan dengan berbagai kemungkinan soal yang berbeda.












