Soal-Soal Statistika kelas 12 Dan Pembahasannya
Soal Statistika kelas 12
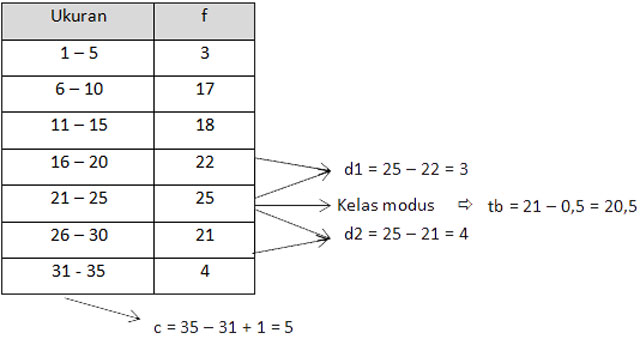
1. Modus dari data pada tabel berikut adalah …
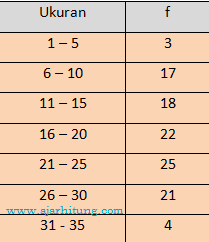
a. 20,5 + ¾ .5
b. 20,5 + 3/25 .5
c. 20,5 + 3/7 .5
d. 20,5 – ¾ .5
e. 20,5 – 3/7 .5
Pembahasan:
Rumus modus untuk data kelompok adalah:

Dengan:
tb = tepi bawah
d1 = selisih frekuensi kelas modus dengan kelas sebelumnya
d2 = selisih frekuensi kelas modus dengan kelas sesudahnya
c = panjang kelas
Pada soal diketahui data:

Sehingga nilai modus dapat kita cari:

Mo = 20,5 + 3/7.5
Jawaban: C
2. Modus dari data pada tabel distribusi frekuensi berikut adalah …

a. 34,50
b. 35,50
c. 35,75
d. 36,25
e. 36,50
Pembahasan:
Rumus modus untuk data kelompok adalah:

Dengan:
tb = tepi bawah
d1 = selisih frekuensi kelas modus dengan kelas sebelumnya
d2 = selisih frekuensi kelas modus dengan kelas sesudahnya
c = panjang kelas
Pada soal diketahui data:
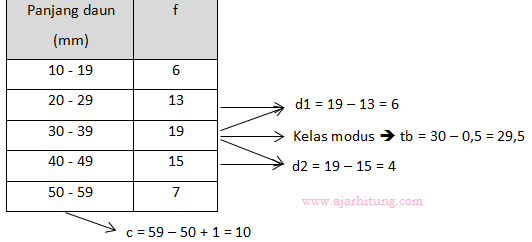
Sehingga nilai modus dapat kita cari:

Mo = 29,5 + 6/10.10
Mo = 29,5 + 6
Mo = 35,5
Jawaban: B
3. Simpangan baku dari data 2, 3, 4, 5, 6 adalah …
a. √15
b. √10
c. √5
d. √3
e. √2
Pembahasan:
Rumus untuk mencari simpangan baku adalah:

Dengan:
S = simpangan baku
xi = data
x ̅ = rata-rata data
n= banyak data
Sebelumnya kita cari dulu rata-ratanya:
x ̅ = (2+3+4+5+6)/5 = 20/5 = 4
Simpangan bakunya (S) =

= √2
Jawaban: E
4. Frekuensi histogram di bawah ini menunjukkan nilai tes matematika sekelompok siswa SMA kelas XII-IPS. Rata-rata nilai raport tersebut adalah …


Pembahasan:
Kita ubah data dalam histogram di atas dalam bentuk tabel:

Rumus rata-rata dengan data kelompok adalah:

Jawaban: D
5. Dalam suatu kelas terdapat siswa sebanyak 21 orang. Nilai rata-ratanya 6, jika siswa yang paling rendah nilainya tidak dikutsertakan, maka nilai rata-ratanya menjadi 6,2. Nilai yang terendah tersebut adalah …
a. 0
b. 1
c. 2
d. 3
e. 4
Pembahasan:
Nilai rata-rata 21 orang = 21 x 6 = 126
Nilai rata-rata 20 orang = 20 x 6,2 = 124
Nilai anak yang terendah = 126 – 124 = 2
Jawaban: C
6. Simpangan baku dari data 7, 7, 6 , 11, 7, 5, 6, 7 adalah…
a. ½ √11
b. ½ √13
c. ½ √15
d. ½ √17
e. ½ √19
Pembahasan:
Rumus untuk mencari simpangan baku adalah:

Dengan:
S = simpangan baku
xi = data
x ̅ = rata-rata data
n= banyak data
Sebelumnya kita cari dulu rata-ratanya:

Simpangan bakunya (S) =

Jawaban: A
7. Diagram lingkaran di bawah ini menunjukkan hobi dari siswa kelas XII IPS SMA. Jika diketahui 60 siswa hobi menonton. Banyak siswa yang hobinya membaca adalah …

a. 60 siswa
b. 120 siswa
c. 180 siswa
d. 200 siswa
e. 220 siswa
Pembahasan:
Siswa yang hobi membaca = 3600 – (700 + 1100 + 300 + 900) = 600
Banyak siswa yang hobi membaca = 60/30 x 60 = 120 siswa
Jawaban: B
8. Nilai rata-rata dari tabel di bawah ini adalah …

a. 61
b. 62
c. 63
d. 64
e. 65
Pembahasan:
Rumus rata-rata dengan data kelompok adalah:

Maka:
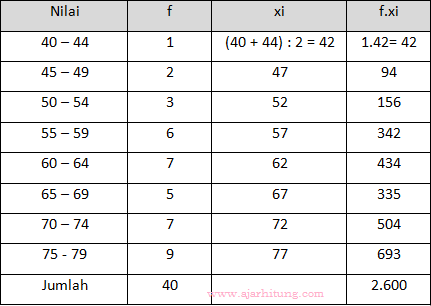
Sehingga rata-ratanya:
x ̅ = 2600/40
x ̅ = 65
Jawaban: E
9. Rata-rata sekelompok bilangan adalah 40. Ada bilangan yang sebenarnya 60, tetapi terbaca 30. Setelah dihitung kembali ternyata rata-rata yang benar adalah 41. Banyak bilangan dalam kelompok itu adalah …
a. 20
b. 25
c. 30
d. 42
e. 45
Pembahasan:
Banyak bilangan = n
Jumlah total bilangan = 40 x n = 40n
Selisih kesalahan baca = 60 – 30 = 30
Jumlah nilai yang sebenarnya = 40n + 30
Rata-rata yang sebenarnya = (40n+30)/n
41 = (40n+30)/n
41n = 40n + 30
n = 30
jadi, banyaknya bilangan ada 30.
Jawaban: C
10. Banyak siswa kelas A adalah 30. Kelas B adalah 20 siswa. Nilai rata-rata ujian matematika kelas A lebih 10 dari kelas B. Jika rata-rata nilai ujian matematika gabungan dari kelas A dan kelas B adalah 66, maka rata-rata nilai ujian matematika kelas B adalah …
a. 58
b. 60
c. 62
d. 64
e. 66
Pembahasan:
Banyak siswa kelas A = nA = 30
Banyak siswa kelas B = nB = 20
Rata-rata kelas A = xA = 10 + xB
Rata-rata kelas B = xB
Xgab = 66

3300 = 30xB + 300 + 20xB
3000 = 50xB
xB = 60
Jadi, rata-rata kelas B adalah 60
Jawaban: B
11. Umur rata-rata dari suatu kelompok yang terdiri dari guru dan dosen adalah 42 tahun. Jika umur rata-rata para guru 39 tahun dan umur rata-rata para dosen 47 tahun, maka perbandingan banyaknya guru dan banyaknya dosen adalah …
a. 5 : 3
b. 5 : 4
c. 3 : 4
d. 3 : 5
e. 3 : 7
Pembahasan:
Banyak guru = x
Banyak dosen = y
Jumlah umur guru = 39x
Jumlah umur dosen = 47x
Rata-rata gabungan = 42
Jumlah umur gabungan = 42 (x + y)
Maka:
Jumlah umur guru + dosen = jumlah umur gabungan
39x + 47x = 42(x + y)
39x + 47x = 42x + 42y
5y = 3x
x/y = 5/3
jadi, perbandingan guru : dosen = 5 : 3
Jawaban: A
12. Dua kelompok anak masing-masing terdiri dari 4 anak, mempunyai rata-rata berat badan 30 kg dan 33 kg. Kalau seorang anak dari masing-masing kelompok ditukarkan maka ternyata rata-rata berat badan menjadi sama sama. Selisih berat badan yang ditukarkan adalah …
a. 1 1/2
b. 2
c. 4
d. 6
e. 8
Pembahasan:
Jumlah anak kelompok 1 = x
Jumlah anak kelompok 2 = y
n1 = n2 = 4
Rata-rata kelompok 1 = x1 = 30
Jumlah berat badan kelompok 1 = 30 x 4 = 120
Rata-rata kelompok 2 = x2 = 33
Jumlah berat badan kelompok 2 = 33 x 4 = 132
Rata-rata setelah ada pertukaran =

120 – x + y = 120 – y + x
2y – 2x = 132 – 120
2y – 2x = 12
y – x = 6
Jadi, selisih berat badan yang ditukar adalah 6 kg.
Jawaban: D
13. Sumbangan rata-rata dari 25 keluarga adalah Rp35.000,-. Jika besar sumbangan seorang warga bernama ‘Noyo’ digabungkan dengan kelompok tersebut maka sumbangan rata-rata dari 26 keluarga sekarang menjadi Rp36.000,- ini berarti bahwa sumbangan ‘Noyo’ sebesar …
a. Rp45.000,-
b. Rp53.000,-
c. Rp56.000,-
d. Rp61.000,-
e. Rp71.000,-
Pembahasan:
Jumlah sumbangan 25 keluarga = 25 x Rp35.000 = Rp875.000
Jumlah sumbangan 26 keluarga = 26 x Rp36.000 = Rp936.000
Besar sumbangan Noyo = Rp936.000 – Rp875.000 = Rp61.000
Jawaban: D
14. Dalam suatu ujian, perbandingan jumlah siswa pria dan wanita adalah 6 : 5. Diketahui 3 peserta pria dan 1 peserta wanita tidak lulus. Jika perbandingan jumlah peserta pria dan wanita yang lulus ujian adalah 9 : 8 maka jumlah peserta yang lulus adalah …
a. 26
b. 30
c. 51
d. 54
e. 55
Pembahasan:
Banyak peserta pria = x
Banyak peserta wanita = y
Pria : wanita = 6 : 5
x/y = 6/5
5x = 6y
y = 5x/6 …. (i)
3 pria dan 1 wanita tidak lulus, maka yang lulus =
Pria = x – 3
Wanita = y – 1
Pria lulus : wanita lulus = 9 : 8

8x – 24 = 9y – 9
8x – 9y = 15 … (ii)
Subtitusikan (i) dalam (ii)
8x – 9y = 15
8x – 9.5x/6 = 15
8x – 15x/2 = 15 (kali 2)
16x – 15x = 30
x = 30
y = 5x/6 = 5.30/6 = 25
Jadi, banyak peserta yang lulus adalah = (x – 3) + (y – 1) = (30 – 3) + (25 – 1) = 27 + 24 = 51
Jawaban: C
15. Dari nilai ulangan 12 siswa, diketahui nilai terkecil 20 dan nilai terbesar 80, nilai rata-rata ulangan siswa tersebut tidak mungkin sama dengan …
a. 22
b. 25
c. 36
d. 38
e. 32
Pembahasan:
– Jika 11 orang mendapat nilai 20 dan 1 orang mendapat nilai 80, maka rata-ratanya:
((11×20)+(1×80))/12=(220+80)/12=300/12=25
– Jika 1 siswa mendapat nilai 20 dan 11 siswa mendapar nilai 80, maka rata-ratanya:
((1×20)+(11×80))/12=(20+880)/12=900/12=75
Sehingga batas rata-ratanya adalah: 25 ≤ x ≤ 75
Maka, rata-rata yang tidak mungkin adalah 22
Jawaban: A
16. Suatu data dengan rata-rata 16 dan jangkauan 6. Jika setiap nilai dalam data dikalikan p kemudian dikurangi q didapat data baru dengan rata-rata 20 dan jangkauan 9. Nilai dari 2p + q = …
a. 3
b. 4
c. 7
d. 8
e. 9
Pembahasan:
Misal datanya: x1, x2, x3, …, xn
Rata-ratanya = 
Jangkauan = xn – x1 = 6
Jika setiap data dikali p lalu dikurangi q:
Rata-ratanya =

= 16p – q = 20 … (i)
Jangkauan = (xn.p – q) – (x1.p – q) = 9
= (xn – x1)p = 9
= 6p = 9
= p = 9/6 …(ii)
Subtitusikan (ii) dalam (i):
16.9/6 – q = 20
24 – q = 20
q = 4
jadi, nilai 2p + q = 2.9/6 + 4 = 3 + 4 = 7
Jawaban: C
17. Diagram berikut menunjukkan persentase kelulusan siswa tiga sekolah selama empat tahun.

Pernyataan berikut yang benar berdasarkan diagram di atas adalah …
a. Rata-rata persentase kelulusan sekolah golongan C terbaik
b. Persentase kelulusan sekolah C selalu berada diposisi kedua
c. Persentase kelulusan sekolah C selalu lebih baik dari sekolah A
d. Persentase kelulusan sekolah B selalu lebih baik dari sekolah C
e. Persentase kelulusan sekolah C selalu lebih baik dari pada tahun sebelumnya.
Pembahasan:
Sebelumnya mari kita cari rata-rata masing-masing sekolah:
– Rata-rata sekolah A
= (57 + 65 + 83 + 77) : 4 = 70,5
– Rata-rata sekolah B
= (90 + 90 + 95 + 95) : 4 = 92,5
– Rata-rata sekolah C
= (69 + 78 + 79 + 100) : 4 = 81,6
Selanjutnya kita bahas masing-masing opsi:
Opsi A salah, karena rata-rata terbaik adalah sekolah B
Opsi B salah, karena pada tahun ke-4 persentase sekolah C adalah yang pertama
Opsi C salah
Opsi D salah, karena pada tahun ke-4 B di bawah C
Opsi E benar
Jawaban: E
18. Dari 3 bilangan yang terkecil adalah 19 dan yang terbesar 75. Rata-rata hitung ketiga bilangan tersebut tidak mungkin sama dengan …
a. 49
b. 52
c. 53
d. 56
e. 59
Pembahasan:
Bilangan yang dimaksud: 19, a, 75
– Rata-rata terkecil misalkan ketika a = 19
(19 + 19 + 75) : 3 = 37,67
– Rata-rata terbesar misalkan ketika a = 75
(19 + 75 + 75) : 3 = 56,33
Jadi: batas nilai rata-ratanya adalah: 37,67 ≤ x ≤ 56,33
Maka, rata-ratanya tidak mungkin 59
Jawaban: E
19. Nilai rata-rata ulangan matematika dari kedua kelas adalah 5,38. Jika nilai rata-rata kelas pertama yang terdiri dari 38 siswa adalah 5,8 dan kelas kedua terdiri dari 42 siswa maka nilai rata-rata kelas kedua adalah …
a. 5
b. 5,12
c. 5,18
d. 5,21
e. 5,26
Pembahasan:
Rata-rata gabungan = xgab = 5,38
Rata-rata kelas pertama = xA = 5,8
Jumlah siswa A = nA = 38
Jumlah siswa B = nB = 42
Rata-rata gabungan dicari dengan rumus:

5,38 . 80 = 220,4 + 42xB
430,4 = 220,4 + 42xB
430,4 – 220,4 = 42xB
210 = 42xB
xB = 210/42
xB = 5
Jadi, rata-rata kelas kedua adalah 5
Jawaban: A
20. Nilai rata-rata ulangan matematika dari 40 siswa SMA adalah 70. Jika seorang siswa yang nilainya 100 dan 3 orang siswa yang nilainya masing-masing 30 tidak dimasukkan dalam perhitungan maka nilai rata-ratanya menjadi …
a. 70,5
b. 72,5
c. 74,5
d. 75,5
e. 76,5
Pembahasan:
Total nilai seluruh siswa = 40 x 70 = 2.800
Total nilai 36 siswa yang baru = (2.800 – (100 + 3.30)
= 2.800 – 190
= 2.610
Jadi, rata-rata yang baru adalah = 2.610/36 = 72,5
Jawaban: B
21. Tahun yang lalu gaji perbulan 5 orang karyawan dalam ribuan rupiah sebagai berikut: 480, 360, 650, 700, 260. Tahun ini gaji mereka naik 15% bagi yang sebelumnya bergaji kurang dari Rp500.000,00 dan 10% bagi yang sebelumnya bergaji lebih dari Rp500.000,00. Rata-rata besarnya kenaikan gaji mereka per bulan adalah …
a. Rp60.000,-
b. Rp62.000,-
c. Rp63.000,-
d. Rp64.000,-
e. Rp65.000,-
Pembahasan:
Kenaikan gaji 15% untuk yang berpenghasilan < Rp500.000,-
– 480.000 x 15/100 = 72.000
– 360.000 x 15/100 = 54.000
– 260.000 x 15/100 = 39.000
Kenaikan gaji 10% untuk yang berpenghasilan > Rp500.000,-
– 650.000 x 10/100 = 65.000
– 700.000 x 10/100 = 70.000
Rata-rata besarnya kenaikan gaji adalah:
(72.000+54.000+39.000+65.000+70.000)/5=60.000
Jawaban: A
22. Suatu data mempunyai rata-rata 35 dan jangkauan 7. Jika setiap nilai dalam data dikali p kemudian dikurangi q didapat data baru dengan rata-rata 42 dan jangkauan 9. Nilai 7p – q = …
a. 3
b. 4
c. 5
d. 6
e. 7
Pembahasan:
Misal datanya: x1, x2, x3, …, xn
Rata-ratanya 
Jangkauan = xn – x1 = 7
Jika setiap data dikali p lalu dikurangi q:
Rata-ratanya =

= 35p – q = 42 … (i)
Jangkauan = (xn.p – q) – (x1.p – q) = 9
= (xn – x1)p = 9
= 7p = 9
= p = 9/7 …(ii)
Subtitusikan (ii) dalam (i):
35.9/7 – q = 42
45 – q = 42
q = 3
jadi, nilai 7p – q = 7.9/7 – 3 = 9 – 3 = 6
Jawaban: D
23. Diketahui data-data x1, x2, x3, …., x10. Jika setiap nilai ditambah 10, maka…
(1) Rata-rata akan bertambah 10
(2) Jangkauan bertambah 10
(3) Median bertambah 10
(4) Simpangan kuartil bertambah 10
Pembahasan:
– Rata-rata:

– Jangkauan: R = x10 – x1
– Median: 
– Simpangan Kuartil: Qd = ½ (Q3 – Q1) = ½ (x8 – x3)
Jumlah nilai tiap data ditambah 10, maka:
– Rata-rata:

– Jangkauan: R = (x10 + 10) – (x1 + 10)
= x10 – x1
– Median:

– Simpangan Kuartil: Qd = ½ (Q3 – Q1) = ½ (x8+10) – (x3+10)
= ½ (x8 – x3)
= Qd
Mari kita bahas satu persatu opsinya:
Opsi 1 benar, rata-ratanya bertambah 10
Opsi 2 salah, jangkauannya tetap
Opsi 3 benar, mediannya bertambah 10
Opsi 2 salah, simpangan kuartilnya tetap
Jadi, pilihan 1 dan 3 yang benar
24. Sekumpulan data mempunyai rata-rata 12 dan jangkauan 6. Jika setiap data dikurangi dengan a kemudian hasilnya dibagi dengan b ternyata menghasilkan data baru dengan rata-rata 2 dan jangkauan 3, maka nilai a dan b adalah …
a. 8 dan 2
b. 10 dan 2
c. 4 dan 4
d. 6 dan 4
e. 8 dan 4
Pembahasan:
Misal datanya: x1, x2, x3, …, xn
Rata-ratanya 
Jangkauan = xn – x1 = 6
Jika setiap data dikurangi a lalu dibagi b:


Subtitusikan (ii) dalam (i):
(12-a)/b = 2
(12-a)/2 = 2
12-a=4
a = 8
jadi, nilai a dan b adalah 8 dan 2
Jawaban: A
25. Data berikut adalah data tinggi badan sekelompok siswa:

Jika median data di atas adalah 163,5 cm maka nilai k adalah …
a. 20
b. 22
c. 40
d. 46
e. 48
Pembahasan:
Perlu diketahui, bahwa rumus untuk mencari median (Me) adalah:

Dengan:
Me = median
tb = tepi bawah kelas yang memuat median
n = banyak data
f kum.sebelum = frekuensi kumulatif sebelum kelas median
f = frekuensi kelas median
c = panjang kelas
Perhatikan tabel frekuensi kumulatif berikut ini: (data berdasakan soal di atas)

Maka, mediannya:

6k = 40 + 5k
k = 40
Jawaban: C






